Certifying Trajectories in Seconds
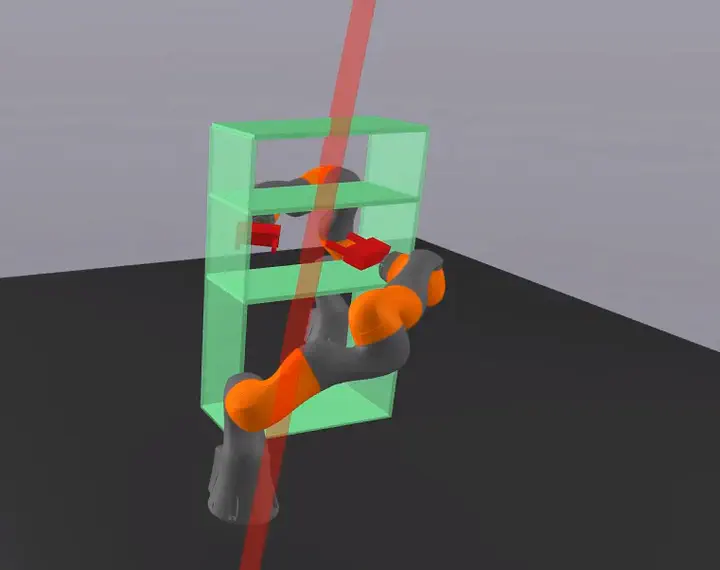 A pair of manipulators reach into a shelf. The red hyperplane certifies that the grippers do not collide at any point during the motion plan.
A pair of manipulators reach into a shelf. The red hyperplane certifies that the grippers do not collide at any point during the motion plan.Motivation
Collision-free motion planning is a fundamental problem in the safe and efficient operation of any robotic system. One of the most important subroutines in collision-free motion planning is collision detection, which has been studied extensively. Algorithms for checking whether a single configuration is collision free are quite mature and can be performed in microseconds on modern hardware.
By contrast, algorithms which are capable of certifying non-collision for the infinite family of configurations along a motion plan are less common. Known as dynamic collision checking, this subroutine is performed hundreds to thousands of times in randomized motion planning methods, and so the speed as well as the correctness of these algorithms is central to their adoption. Due to the speed requirement, it is common practice to heuristically perform dynamic collision checking by sampling a finite number of static configurations along the motion plan. Nevertheless, it is widely recognized that this is insufficient for safety critical robots.
Current methods for formally checking the safety of robots frequently only apply to piecewise linear motion plans and are either too slow for practical deployment, rely on difficult to acquire parameters, or are too conservative for certifying motion plans in tight spaces.
Video Summary
Contribution
In this work, we provide a method for certifying that a robot trajectory contains no collisions. The method provides rigorous proofs of non-collision using Sums-of-Squares optimization, can certify piecewise-polyonmial paths of arbitrary degree, and is efficient enough to certify the safety of a bimanual manipulator motion plan in just over a second. Moreover, it is efficient enough to discriminate the safety of two motion plans which differ by only millimeters.
Results
Complexity of Certification
We consider two realistic robotic scenarios and demonstrate that our method is fast enough to serve as a final safety check of a robot motion plan. Our first system is a bimanual manipula
The complexity of our method scales in the degree of freedom (DOF) of the robot as well as the degree of the path parametrization. We therefore test our method on piecewise linear motion plans for a high DOF plant, the bimanual manipulator interacting with a shelf and piecewise cubic motion plans for a lower DOF plant.
| Bimanual Plant, Piecewise Linear Motion Plan | Single arm plant, Piecewise Cubic Motion Plan |
|---|---|
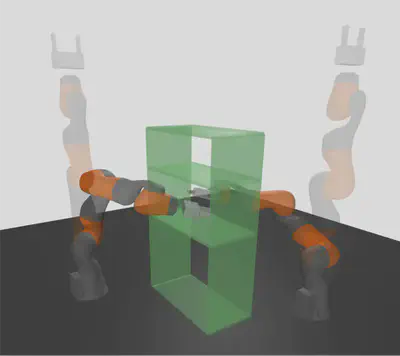 |  |
| Total solver time to certify motion plan: 1.211 sec | Total solver time to certify motion plan: 8.99 sec |
Visualizing the Certificates
The certificates of non-collision can be visualized as hyperplanes in the task space. Click “Open Controls” to turn different hyperplanes on and off, replay the animation, and more.