Abstract
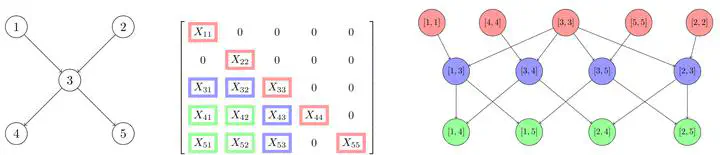
We study a general class of least-squares problems structured according to a partially ordered set (poset). This is a fundamental optimization problem underlying the design of structured controllers on directed acyclic graphs or posets. We show that the optimality conditions of this problem yield a structured linear system, with sparsity pattern determined by a derived poset known as the poset of intervals. In general, this system could be relatively dense, and thus standard sparse linear algebra techniques may fail to provide significant reduction in computational complexity. Nonetheless, for a broad class of posets called multitrees identified in (Nayyar 2015) we show that performing elimination according to an order defined by the poset intervals progressively decouples variables, reducing the arithmetic complexity of solving the problem.