Approximating Robot Configuration Spaces with few Convex Sets using Clique Covers of Visibility Graphs
Abstract
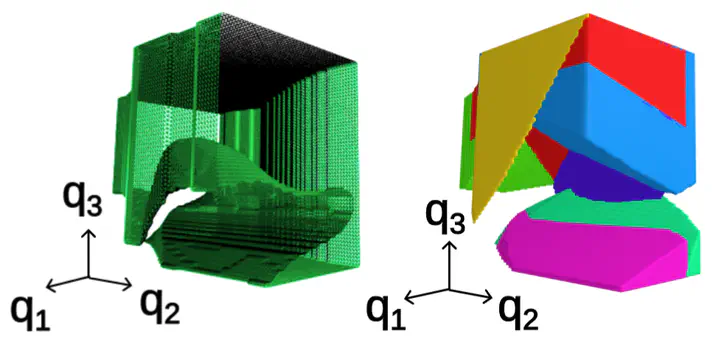
Many computations in robotics can be dramatically accelerated if the robot configuration space is described as a collection of simple sets. For example, recently developed motion planners rely on a convex decomposition of the free space to design collision-free trajectories using fast convex optimization. In this work, we present an efficient method for approximately covering complex configuration spaces with a small number of polytopes. The approach constructs a visibility graph using sampling and generates a clique cover of this graph to find clusters of samples that have mutual line of sight. These clusters are then inflated into large, full-dimensional, polytopes. We evaluate our method on a variety of robotic systems and show that it consistently covers larger portions of free configuration space, with fewer polytopes, and in a fraction of the time compared to previous methods.